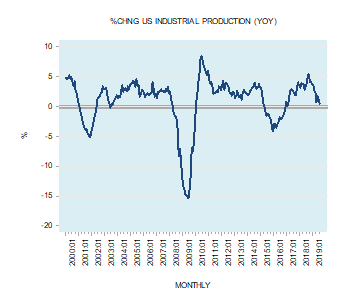
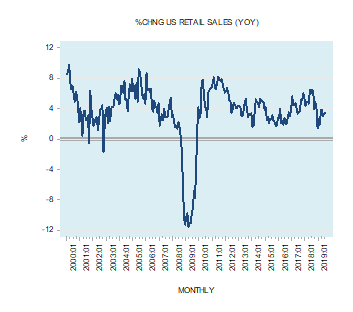
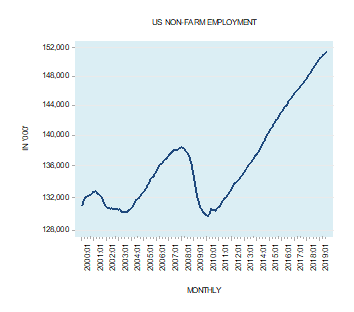
In response to a weakening in the yearly growth rate of key economic indicators such as industrial production and real gross domestic product (GDP) some commentators have raised the alarm of the possibility of a recession emerging.
|
|
|
Some other commentators are dismissive of this arguing that the likelihood of a recession ahead is not very high given that other important indicators such as consumer outlays as depicted by the annual growth rate of retail sales and the state of employment appear to be in good shape (see charts).
|
|
|
Most experts tend to assess the strength of an economy in terms of real gross domestic product (GDP), which supposedly mirrors the total amount of final goods and services produced.
To calculate a total, several things must be added together. In order to add things together, they must have some unit in common. It is not possible however to add refrigerators to cars and shirts to obtain the total amount of final goods.
Since total real output cannot be defined in a meaningful way, obviously it cannot be quantified. To overcome this problem economists employ total monetary expenditure on goods, which they divide by an average price of goods. However, is the calculation of an average price possible?
Suppose two transactions are conducted. In the first transaction, one TV set is exchanged for $1,000. In the second transaction, one shirt is exchanged for $40. The price or the rate of exchange in the first transaction is $1000/1TV set. The price in the second transaction is $40/1shirt. In order to calculate the average price, we must add these two ratios and divide them by 2. However, $1000/1TV set cannot be added to $40/1shirt, implying that it is not possible to establish an average price.
On this Rothbard wrote,
Thus, any concept of average price level involves adding or multiplying quantities of completely different units of goods, such as butter, hats, sugar, etc., and is therefore meaningless and illegitimate.[1]
Since GDP is expressed in dollar terms, which are deflated by a dubious price deflator, it is obvious that the so called real GDP fluctuations mirror fluctuations in the amount of dollars pumped into the economy.
Hence, various statements by government statisticians regarding the growth rate of the real economy are nothing more than a reflection of the fluctuations in the growth rate of the money supply.
Now, once a recession is assessed in terms of real GDP it is not surprising that the central bank appears to be able to counter the recessionary effects that emerge. For instance, by pushing more money into the economy the central bank’s actions would appear to be effective since real GDP will show a positive response to this pumping after a time lag. (Remember that changes in real GDP reflect changes in money supply).
This means that if the economy can be expressed through indicators such as GDP, then this will allow the central bank to appear to be able to navigate the economy (i.e., GDP) by means of a suitable policy mix. In addition, it makes sense to demand that the central bank should interfere in order to help the economy.
Why business cycles are recurrent?
Even if one were to accept that real GDP is not a fiction and depicts the so-called true economy there is still a problem as to why recessions are of a recurrent nature. Is it possible that it is only external shocks that cause this repetitive occurrence of recessions? Surely, there must be a mechanism here that gives rise to this repetitive occurrence?
In a free market, we could envisage that the economy would be subject to various shocks but it is difficult to envisage a phenomenon of recurrent boom-bust cycles. According to Rothbard,
Before the Industrial Revolution in approximately the late 18th century, there were no regularly recurring booms and depressions. There would be a sudden economic crisis whenever some king made war or confiscated the property of his subjects; but there was no sign of the peculiarly modern phenomena of general and fairly regular swings in business fortunes, of expansions and contractions.[2]
The boom-bust cycle phenomenon is somehow linked to the modern world. But what is the link? The source of recurrent recessions turns out to be the alleged “protector” of the economy — the central bank itself.
We suggest that the phenomenon of recessions is not about the weakness of the economy as such but about the liquidation of various activities that sprang up on the back of the loose monetary policies of the central bank. Here is why.
A loose central bank monetary policy, which results in an expansion of money out of “thin air” sets in motion an exchange of nothing for something, which amounts to a diversion of real wealth from wealth-generating activities to non-wealth-generating activities. In the process, this diversion weakens wealth generators, and this in turn weakens their ability to grow the overall pool of real wealth.
The expansion in activities that emerge from the loose monetary policy is what an economic “boom” (or false economic prosperity) is all about. Note that an increase in the monetary pumping due to loose monetary policy of the central bank lifts the monetary turnover and hence GDP.
Once this monetary turnover is deflated by the so-called average price index this will manifest itself in terms of a strengthening in real GDP. Most experts and commentator are likely to proclaim that the central bank’s loose monetary policies were successful in growing the economy.
Once however, the central bank tightens its monetary stance, this slows down the diversion of real wealth from wealth producers to non-wealth producers. Activities that sprang up on the back of the previous loose monetary policy are now getting less support from the money supply – they fall into trouble and an economic bust or recession emerges in terms of the monetary turnover deflated by the average price index i.e. the growth rate of real GDP comes under downward pressure.
Activities that emerged on the back of previous loose monetary policy cannot now divert real wealth to support themselves. This is because these activities were never economically viable – they could not support themselves without the diversion of real wealth to them by means of an expansion in money supply. Consequently, most of these activities are likely to perish or barely survive.
Could these activities escape the consequences of a bust if they are well managed and have solid appearance? For instance, as a result of the loose monetary stance on the part of the Fed various activities emerge to accommodate the demand for goods and services of the first receivers of newly injected money.
Now, even if these activities are well managed, and maintain very efficient inventory control, this fact cannot be of much help once the central bank reverses its loose monetary stance. These activities are the product of the loose monetary stance of the central bank and they were never approved by the market as such. They emerged on account of the increase in money supply, which gave rise to an increased demand for goods.
Once the central bank monetary stance is reversed, regardless of efficient inventory management, these activities will come under pressure and run the risk of being liquidated. The supply of real savings is not large enough to support these activities.
From what was said we could conclude that recessions are about the liquidation of economic activities that emerged on the back of the loose monetary policy of the central bank. This recessionary process is set in motion when the central bank reverses its earlier loose stance. Note that recession is good news for wealth generators since less real wealth is now being taken from them.
This means that central bank’s ongoing policies that are aimed at mitigating the consequences that arise from its earlier attempts at stabilizing the so-called economy, i.e., real GDP, are key factors behind the repetitive boom-bust cycles. Because of the variable time lags from changes in money to changes in prices and changes in real GDP, Fed policy makers are confronted with economic data that could be in conflict with the Fed’s targets. Hence, this forces central bank officials to respond to the effects of their own previous monetary policies.
Note that Fed policy makers regard themselves as being responsible to bring the so-called economy onto a path of stable economic growth and stable price inflation. Consequently, any deviation from the stable growth path as outlined by policy makers sets the Fed’s response in terms of either tighter or looser stance. These responses to the effects of past policies give rise to fluctuations in the growth rate of the money supply and in turn to recurrent boom-bust cycles.
We hold that the downtrend in the yearly growth rate in the adjusted money supply (AMS) during 2002 to 2007 was responsible for the economic slump of 2008. An uptrend in the growth rate of AMS during 2008 to 2011 provided a support for the strengthening in economic activity until very recently. A visible decline in the annual growth rate in AMS since 2012 has set in motion an economic slump. We suspect that this slump is likely to strengthen as time goes by.
|
|
We suggest that even if the Fed were to lift aggressively its monetary pumping it will not be possible to reverse the downtrend in the AMS growth rate instantly. The state of the pool of real wealth is going to determine the severity of the downturn. We suggest that prolonged reckless monetary and fiscal policies have likely severely undermined the process of real wealth generation. This in turn raises the likelihood that the pool of real wealth is hardly growing. Consequently, it will not surprise us that the likely emerging economic downturn is going to be quite severe by most historical standards.
It is now popular to blame the policies of the US President Trump in particular his trade war with China as the key factor behind a possible recession ahead. Whilst President Trumps’ policies are not in the spirit of the free market, we suggest that the downtrend in the AMS annual growth rate since 2012 has nothing to do with President Trump’s policies but with the policies of the Fed.
Conclusions
Recessions, which are set in motion by a tight monetary stance of the central bank, are about the liquidations of activities that sprang up on the back of the previous loose monetary policies. Rather than paying attention to the so-called strength of real GDP to ascertain where the economy is heading, it will be more helpful to pay attention to the growth rate of the money supply.
By following the growth rate of the money supply, one can ascertain the pace of damage to the real economy that central bank policies inflict. Thus, the increase in the growth momentum of money should mean that the pace of wealth destruction is intensifying. Conversely, a fall in the growth momentum of money should mean that the pace of wealth destruction is weakening.
We suggest that the real GDP growth rate does not measure the real strength of an economy but rather reflects monetary turnover adjusted by a dubious statistic called the price deflator. Obviously then the more money is pumped, all other things being equal, the stronger the economy appears to be. In this framework of thinking one is not surprised that the Fed can “drive” the economy since by means of monetary pumping the central bank can influence the GDP growth rate. By means of the real GDP statistic Fed policy makers and government officials can create an illusion that they can grow the economy. In reality the policy of intervention of the Fed and the government can only deepen the economic impoverishment by weakening wealth generators.
It now seems to be the consensus that the key factor behind a possible recession ahead would be the policies of the US President Trump in particular his trade war with China as. However we suggest that a key cause behind the possible recession had already been set in motion by the downtrend in the AMS annual growth rate since 2012. This downtrend has nothing to do with President Trump’s current policies but with the past policies of the Fed.
[1] Murray N.Rothbard, Man Economy and State, Nash Publishing p 734.
[2] Rothbard The Austrian Theory of the Trade Cycle and other essays, The Mises Institute,1983.